6 Checking Assumptions2

6.1 Checking Normality Assumptions

Shapiro-Wilk Test

The Shapiro-Wilk test tests the null hypothesis that the samples come from a normal distribution against the alternative hypothesis that the samples do not come from a normal distribution.

oneway_data[-1,] %>% 
  rstatix::shapiro_test(Colorless,Pink,Orange,Green)
## # A tibble: 4 x 3
##   variable  statistic     p
##   <chr>         <dbl> <dbl>
## 1 Colorless     0.913 0.499
## 2 Green         0.881 0.342
## 3 Orange        0.965 0.813
## 4 Pink          0.937 0.635
shapiro.test(residuals(object = one_aov))
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(object = one_aov)
## W = 0.92472, p-value = 0.1222

QQ Plots

clean_oneway_data %>% 
  mutate(Residual = one_aov$residuals) %>% 
  ggplot(aes(sample = Residual)) + 
  stat_qq() + 
  stat_qq_line() + 
  facet_wrap(~Type)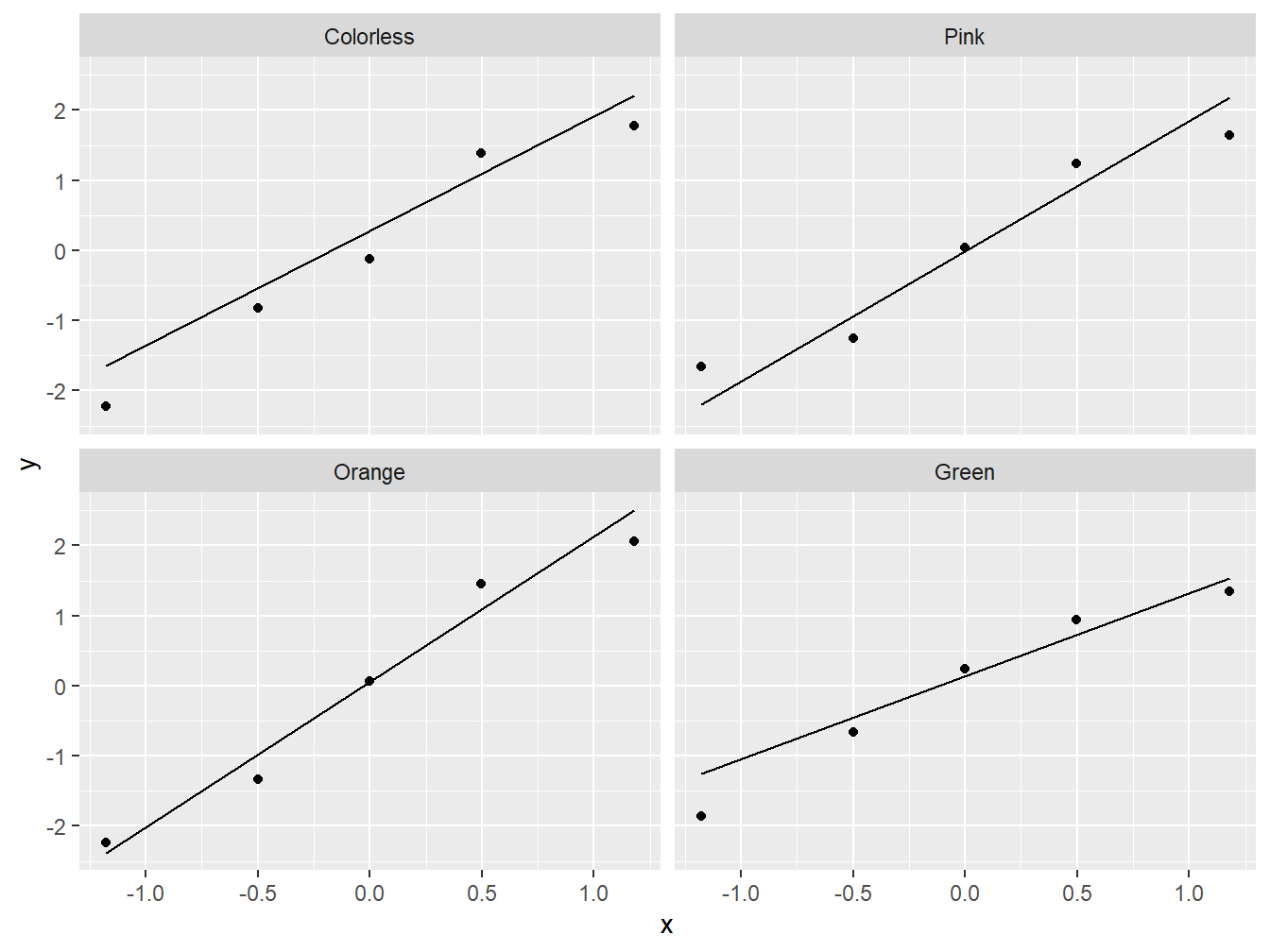

plot(one_aov,2)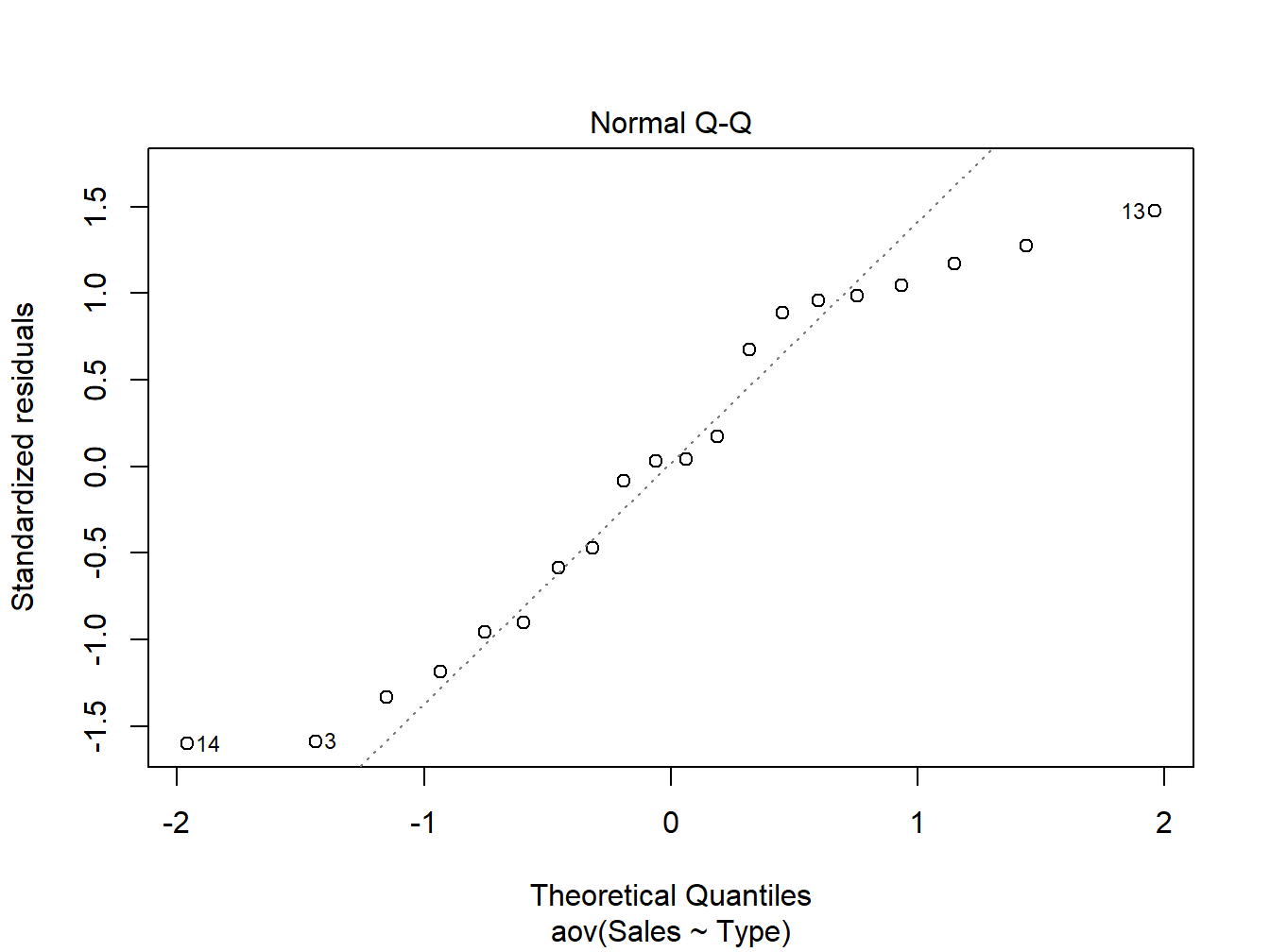

Histogram

clean_oneway_data %>% 
  ggplot(aes(x = Sales)) + 
  geom_histogram(bins = 30, color = "white") + 
  geom_density() + 
  facet_wrap(~Type)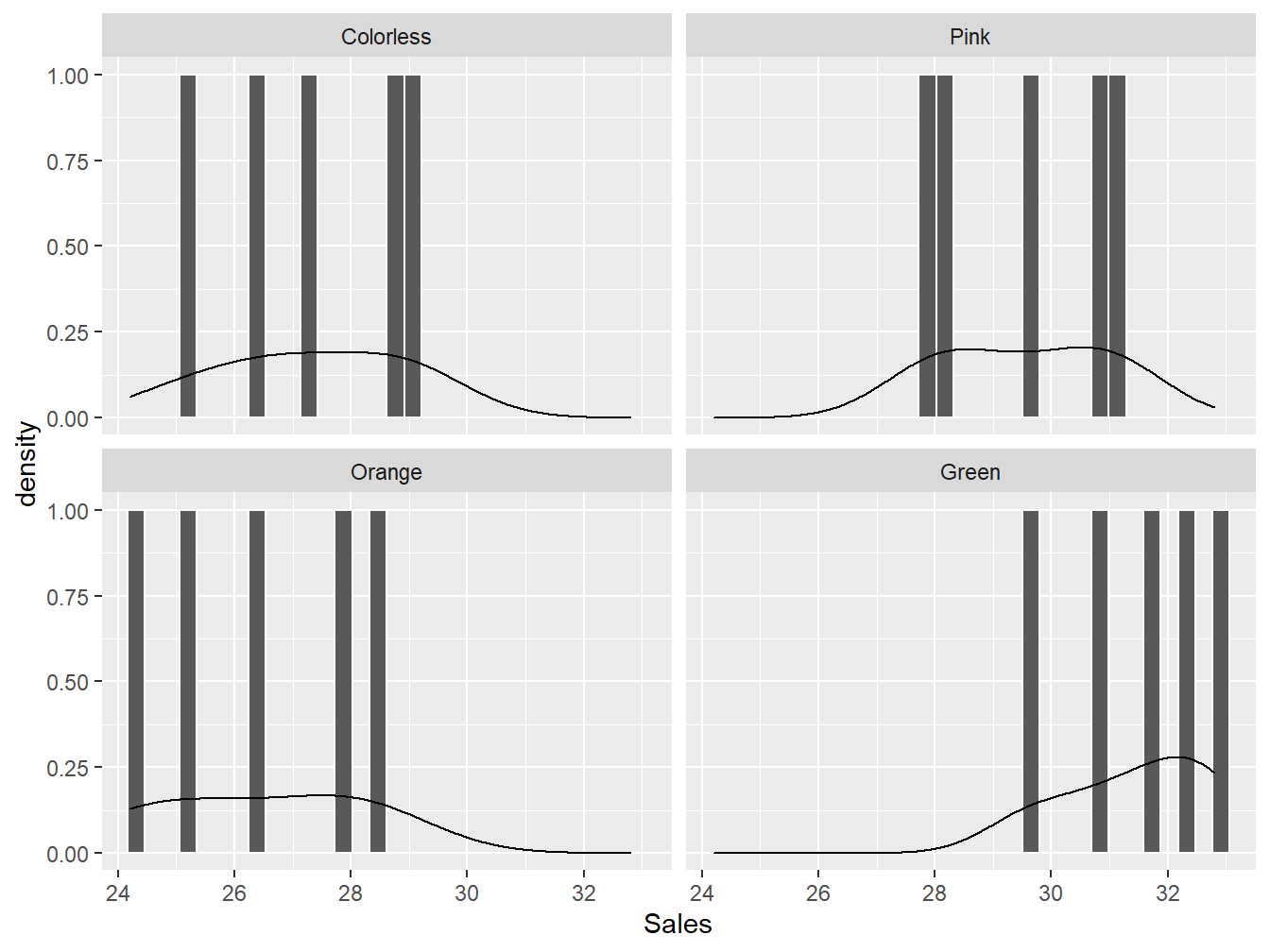

6.2 Checking Homogeneity of Variance Assumption

Bartlet’s Test

Bartlett’s test tests the null hypothesis that the group variances are equal against the alternative hypothesis that the group variances are not equal.

clean_oneway_data %>% 
  bartlett.test(Sales ~ Type, data = .)
## 
##  Bartlett test of homogeneity of variances
## 
## data:  Sales by Type
## Bartlett's K-squared = 0.46564, df = 3, p-value = 0.9264
clean_oneway_data %>% 
  ggboxplot(x = "Type", y = 'Sales',
            fill = "Type",
            palette = c("white", "pink", "orange", "green")) + 
  theme(legend.position = "none")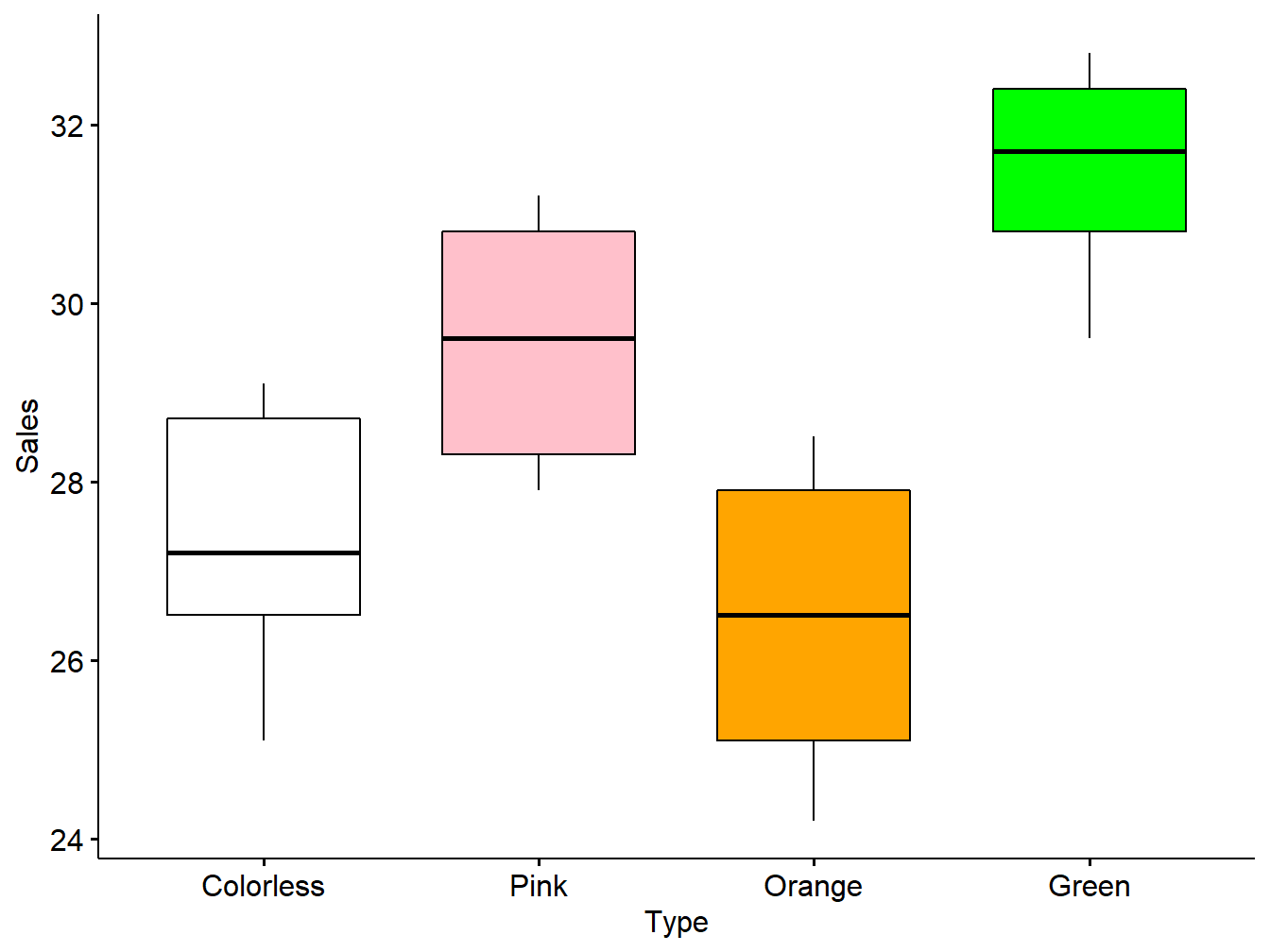

The variability within each group is represented by the vertical size of each box; i.e., the interquartile range (IQR). The boxplot shows that the variability is roughly equal for each group. Let’s look at some more ways to test the homogeneity of variance assumption.

Residual vs. Fitted Values Plot

plot(one_aov,1, las=1)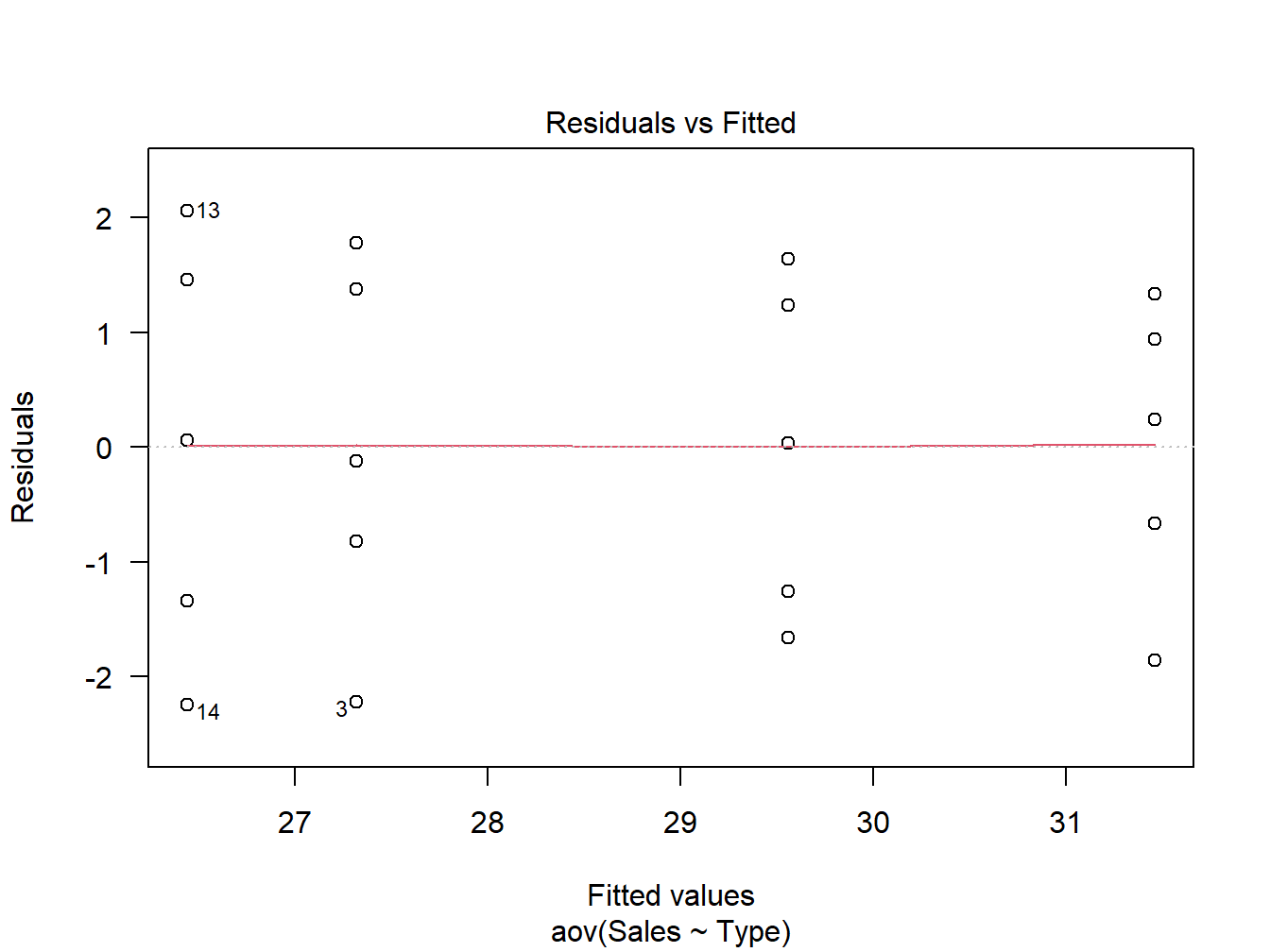

This plot shows the residuals (errors) on the y-axis and the fitted values (predicted values) on the x-axis. If the variance of each group is equal, the plot should show no pattern; in other words, the points should look like a cloud of random points. The plot shows that the variances are approximately homogenous since the residuals are distributed approximately equally above and below zero.

Standardised Residuals vs Fitted values Plot

plot(one_aov,3)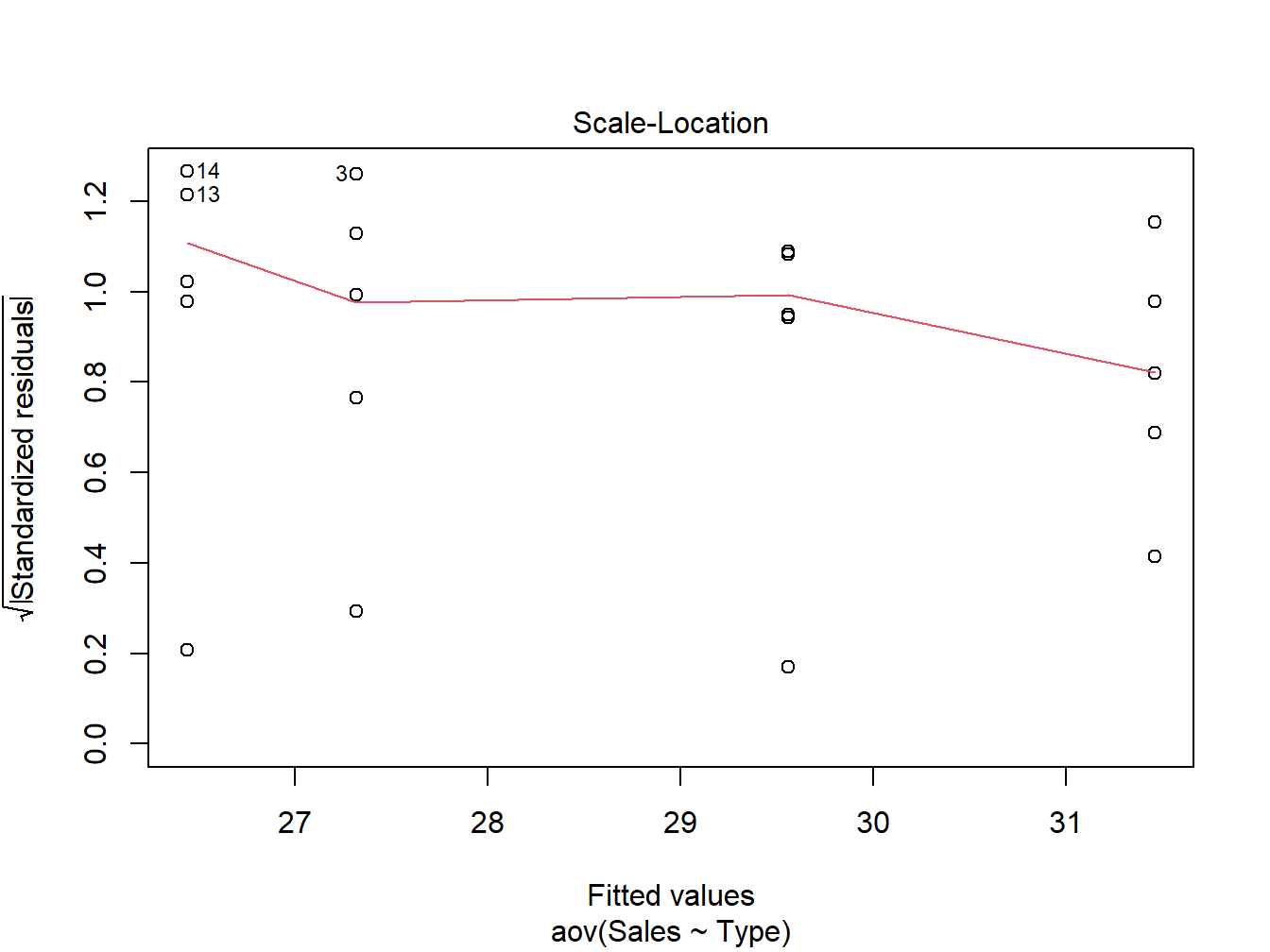

The more coincident the red line plot to the horizontal line at 1, the lesser possibility the violation of the homogeneity of variance assumption.

  1. Except for most of the codes, the contents of this section are obtained from this link↩︎